
Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value.

The open circle symbol \(\circ\) is called the composition operator. We do this by performing the operations with the function outputs, defining the result as the. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. Function composition is only one way to combine existing functions. We read the left-hand side as“\(f\) composed with \(g\) at \(x\),” and the right-hand side as“\(f\) of \(g\) of \(x\).”The two sides of the equation have the same mathematical meaning and are equal. Combining Functions Using Algebraic Operations. We represent this combination by the following notation: The resulting function is known as a composite function. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. When we wanted to compute a heating cost from a day of the year, we created a new function that takes a day as input and yields a cost as output. The order of function composition must be considered when interpreting the meaning of composite functions. (If C C is negative, then this means that the graph shifts over C C to the left.) For example, the graph of y (x 2)2 y ( x 2) 2 is the x2 x 2 -parabola shifted over to have. The function produced by combining two functions is a composite function. If we replace x x by x C x C everywhere it occurs in the formula for f(x) f ( x), then the graph shifts over C C to the right. In other words we want to find where the two. When functions are combined, the output of the first (inner) function becomes the input of the second (outer) function. Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. Example: f (x)x and g (x) (3x) The domain for f (x)x is from 0 onwards: The domain for g (x) (3x) is up to and including 3: So the new domain (after adding or whatever) is from 0 to 3: If we choose any other value, then one or the other part of the new function won't work. So, for instance, if we used the number '25', they would look like this.
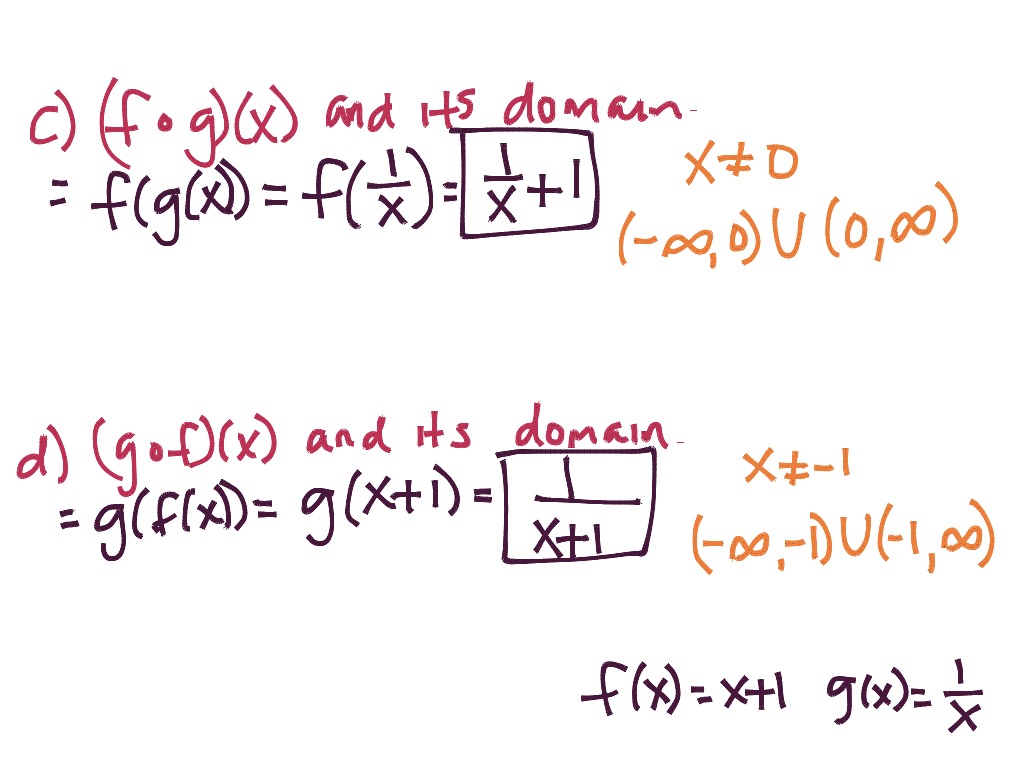
Square root is written with a 'plus or minus' symbol in front, so it looks like this: ''.

\]Ĭreate a Function by Composition of Functions The symbol in the video, '', means 'principle square root'.


 0 kommentar(er)
0 kommentar(er)
